Graph dynamical networks for learning atomic scale dynamics

^{This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. It was originally written as a guest blog for the MLxMIT.}

Understanding the dynamics of atoms in complex materials is an important research problem in materials science, with applications in the design of better batteries, catalysis and membranes. However, extracting the correct information from massive atomic-scale simulation data is challenging, owing to the amorphous (disordered) nature of many materials. In this project, we develop graph dynamical networks (GDyNets) to learn the most important dynamics from time-series molecular dynamics (MD) simulation data. This allows us to learn the dynamics of atoms directly from MD data and provide new scientific insights into important materials.

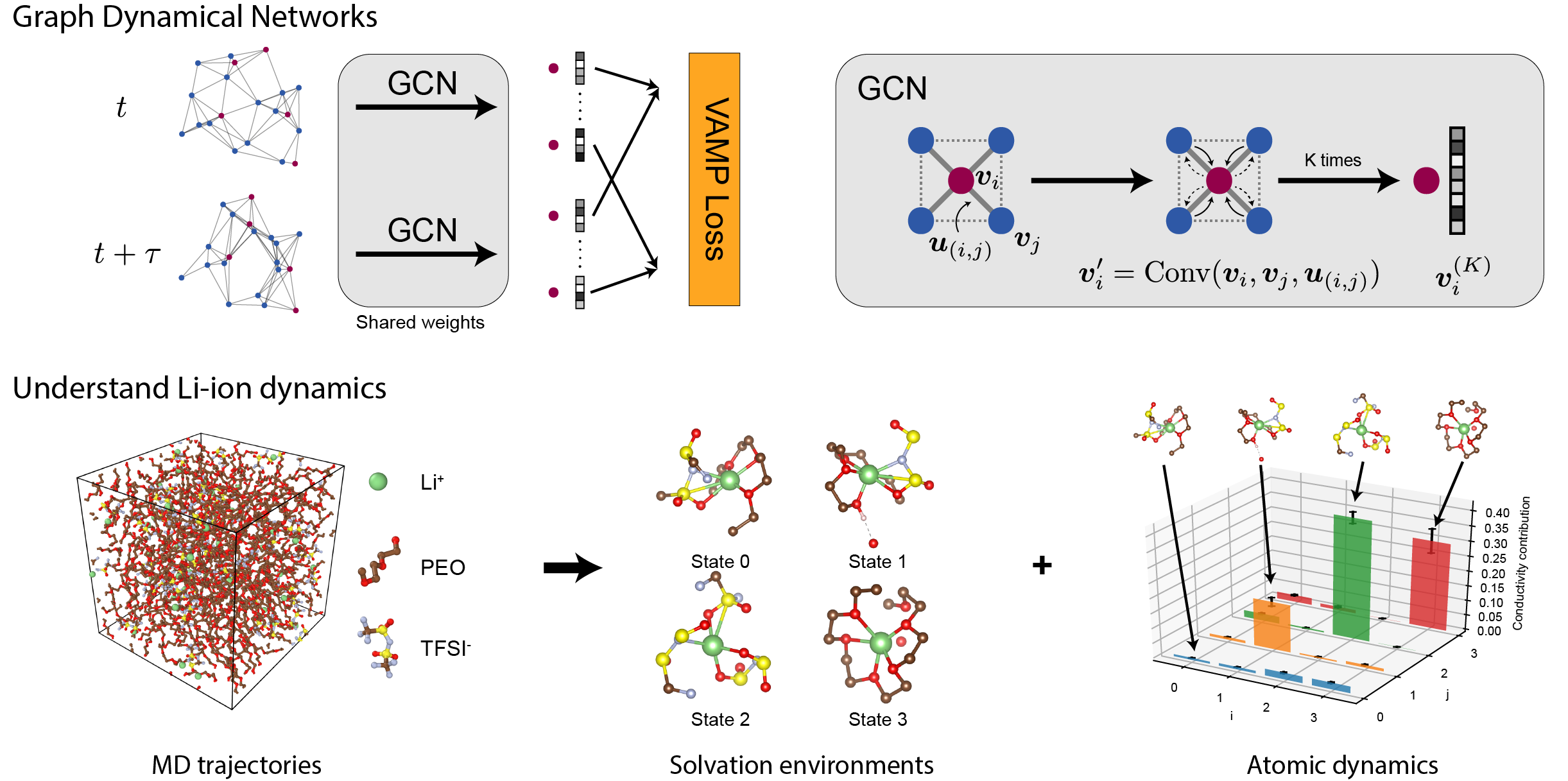
The learning problem can be framed as finding a low dimensional feature space where the non-linear dynamics of atoms can be represented by a linear transition matrix. Assume that the atoms we are interested in follow any non-linear dynamics \(F: x_{t+\tau} = F(x_t)\). We hope to find a mapping function \(\chi(\cdot)\) to map the cartesian coordinates of atoms \(x\) to a low dimensional feature space, such that there exists a low dimensional linear transition matrix \(K: \chi(x_{t+\tau}) \approx K\chi(x_t)\) that can approximate non-linear dynamics of \(F\). Effectively, we are mapping each atom into several “states”, and we can understand their dynamics by analyzing the transition matrix \(K\).

The mapping function \(\chi(\cdot)\) can be learned from time-series MD simulation data \(\{x_t\}\) by minimizing a dynamical loss function (VAMP), but direct learning of \(\chi\) is typically not possible in materials. This is because atoms can move between structurally similar yet distinct chemical environments, making the problem exponentially more complex. We need to encode this symmetry of atoms into the neural networks to solve this problem. We used a type of graph convolutional neural networks (CGCNN) from earlier work to encode the atomic structures in a way that respects the symmetries. In GdyNets, CGCNN is trained with time-series MD data to learn \(\chi\) with a VAMP loss.

We first tested GDyNets in a toy system that has two symmetrically distinct states. We find that GDyNets successfully discover the correct two-state dynamics, while a network that does not respect symmetry learns the wrong dynamics. We then applied the method to a realistic system PEO/LiTFSI, a well-known polymer electrolyte for Li-ion batteries whose transport mechanism is still under debate. We discovered the four most important solvation structure of Li-ion and their dynamics from the MD simulation data and used the results to explain a “negative transference number” recently discovered in experiments.

We find that GDyNets can be used as a general approach to understanding the dynamics of atoms or molecules from the MD simulation data, with potential application to general graph-based data. We have open-sourced our code on GitHub. In the future, we hope to make GDyNets learn non-equilibrium dynamics as well as equilibrium dynamics.