How CGCNN learns 3D structure in materials?

^{This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.}

Last year, we published the work “Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties”, which presents one of the first attempts to encode materials using graph neural networks (along with SchNet). Since then, I was thrilled to see that some researchers started to use CGCNN for different types of materials and improved the methods in many different ways.

However, there is one question which I got asked many times in several conferences about CGCNN – how to build a graph for materials because the definition of bond is ambiguous for inorganic compounds. This is an important question, but we only provided a short explanation in the supplemental information of the original paper. It also relates to some of the key differences between CGCNN and many other works that use graph neural networks for molecules. In this blog, I hope to provide a detailed explanation to this question.

Note: this blog turns out to be much longer than I expected. For a short answer, go to the end of the blog directly.

3D structure is important for materials

One major feature that distincts materials from molecules is that 3D structure can affect material properties significantly. It means that we can’t predict material properties accurately if we don’t encode 3D structure in ML models. One example is SiO2. The chemical bonds in SiO2 are simple: each Si has 4 bonds with O, and each O has 2 bonds with Si. However, there are many different types of SiO2 with vastly different properties. In crystalline forms, Wikipedia listed 14 different types of SiO2 with density ranging from 1.9 - 4.2 g/cm3. Quartz glass, an amorphous form of SiO2, also has properties significantly different from the crystalline forms. This phenomenon happens across almost every type of materials. In polymers, different ways which polymer chains entangle affect their mechanical properties. In molecular crystals, molecules can stack in different orientations to give different electrical properties.

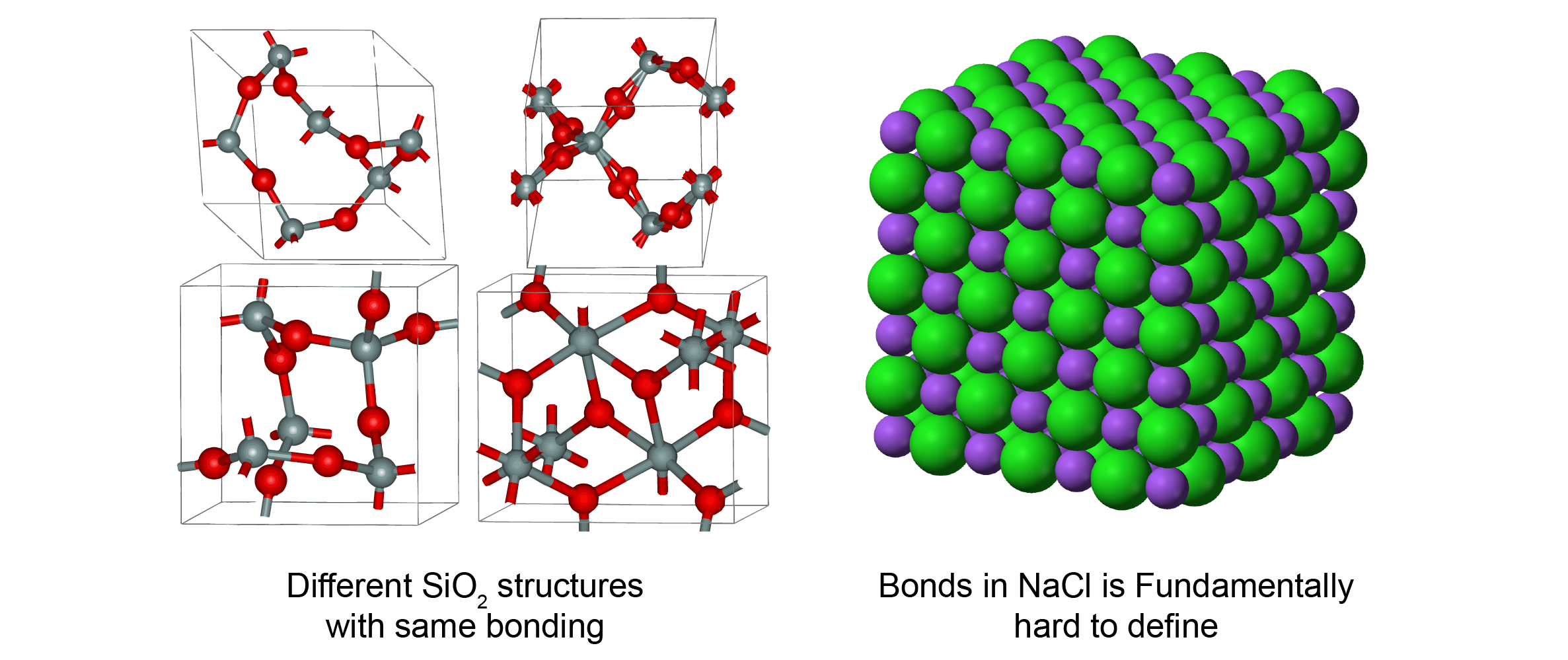
On the other hand, the definition of bonds can be ambiguous in some materials. Fundamentally, inorganic materials can be considered as lots of sphere balls stacked together in 3D space as a result of Coulombic interactions. The the definition of bonds is intrinsically difficult due to the long-range nature of Coulombic forces. The clear definition of bonds in organic molecules is due to the special electronic structure of carbon, which is more like an anormaly rather than the norm. (But this is also why the chemistry about carbon can be so important and complex.) And even in molecular crystals, it is not possible to capture the effect of molecule orientations without considering non-covalent bonds.

As a result of this 3D structure complexity, the simple molecular graph representation, i.e. no edge features or simple one-hot edge features, is not enough for most materials. One should consider materials as a collection of atoms in 3D space rather than a simple 2D graph.

Capture 3D information in CGCNN

In CGCNN, there are three aspects that help us to capture the 3D structural information in materials.

• Graphs are constructed using the nearest neighbor algorithms.
• The edges are encoded with the distance between the two atoms.
• A “gated” architecture is used in the graph neural network to re-weigh the strength of the bonds corresponding to each edge.

These three aspects work together to allow the CGCNN to capture the 3D structural information in materials with a linear computation cost with respect to the size of the system. Now, let’s dive into the details of how they work together.

Locally connected graph

Encoding the edges with distance information is obvious because it is necessary to capture 3D information. It was first proposed by DTNN in 2017 to capture 3D information for molecules. However, in DTNN, the full distance matrix is used, which corresponds to a fully connected graph for the molecules. This doesn’t work well for large material systems because it has a \(O(N^2)\) scalling, and it is less clear how to define the distances in a periodic system. As a result, we used the nearest neighbor algorithm to construct the graphs that represent the 3D structure of materials, which has a \(O(N)\) scalling with respect to the size of the system. In this graph representation, short range interactions are learned directly in each graph convolution operation with nearest neighbors, while long range interactions are learned by propogating information across the graph using multiple graph convolutions. As a result, the entire material system is represented by a locally connected graph corresponding to the 3D structure in periodic box.

Gated architecture

However, this approach alone doesn’t work well for materials without the “gated” architecture in graph neural networks. This is because different neighbors have different interaction strength with the center atom. For inorganic materials, we used 12 nearest neighbors for constructing graphs for all materials, because 12 is the number of neighbors under the closed packing. But different materials will have different number of strong neighbors in their structure. For example, among these 12 nearest neighbors, KCl has 8 neighbors with strong ionic bonds, and NaCl has 6 neighbors with strong ionic bonds. It is very challenging to know which neighbor is important in a more complicated inorganic material. So, we designed a “gated architecture” to learn the importance of neighbors. Specifically, we learn a prefactor between 0 and 1 using the information about the distance between atoms and the types of each atom,

where \(\mathbf{v}_i\), \(\mathbf{v}_j\) are vectors representing atom \(i\) and \(j\), \(\mathbf{u}_{i,j}\) is a vector representing the bond between \(i\) and \(j\), \(\bigoplus\) represents concatenation, \(\sigma\) is a sigmoid function, and \(\mathbf{W}\) and \(\mathbf{b}\) are weights and biases.

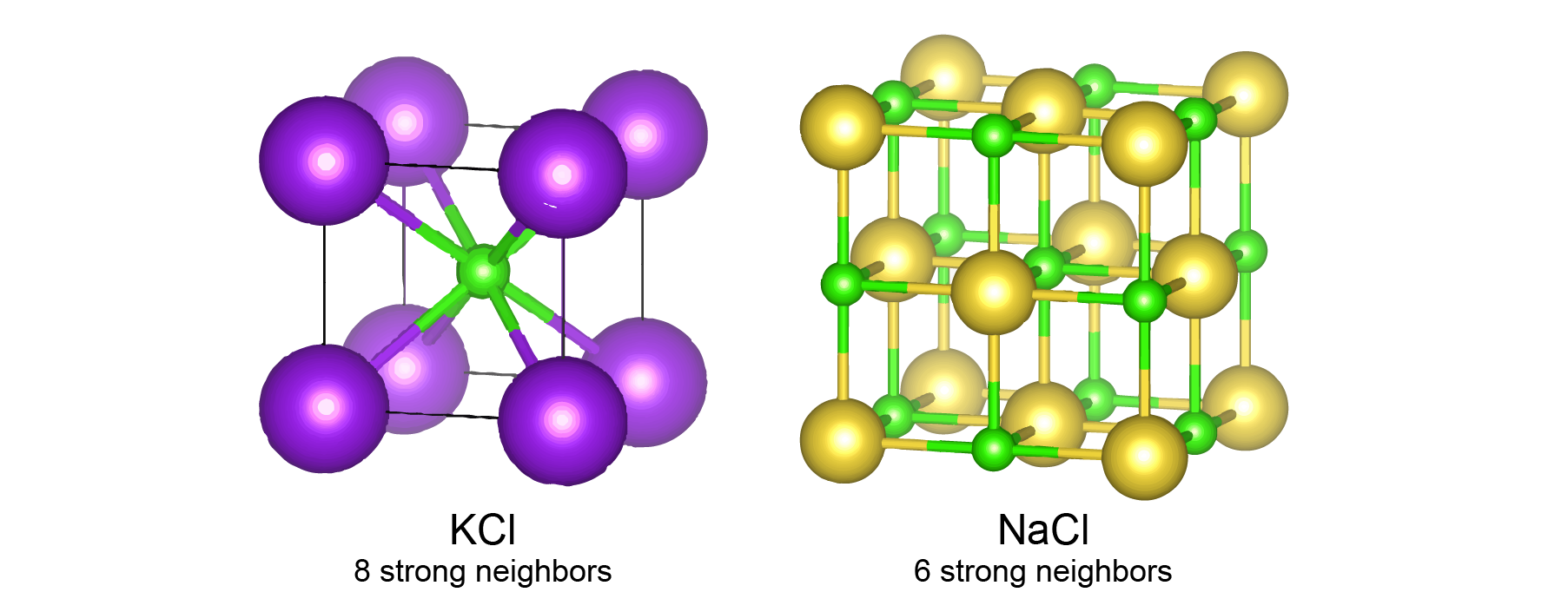
This equation means that after training, the neural network can automatically learn a prefactor that determines the relative importance of the 12 nearest neighbors. For NaCl, the 6 closest neighbors will have a prefactor close to 1, and the rest 6 neighbors will have a prefactor close to 0. For KCl, the 8 closest neighbor will have a prefactor close to 1, and the rest 4 neighbors will have a prefactor close to 0. This prefactor is then used to control the information flow in the graph convolution process.

Combining together

Now, we are ready to answer the question at the begining of this blog.

How to build a graph for materials because the definition of bond is ambiguous for inorganic compounds?

We don’t need to determine if the bond exists between two atoms because the gated achitecture allows us to learn it from data. In CGCNN, the graph topology is defined using the simple nearest neighbor algorithm. However, through an automatically learned prefactor, it can ignore those neighbors that are not important to the center atom.

Broader usage of CGCNN

As we have described, the usage of CGCNN is not limited to inorganic materials. In principle, CGCNN should work for any material with a predefined 3D structure. In our latest work, we applied CGCNN to polymers and liquids in an unsupervised setting and it seems to be pretty succesful.